Để vận dụng và giải các bài tập hình học hoặc ứng dụng vào trong công việc, cuộc sống hàng ngày được hiệu quả, cách tính chu vi tứ giác được chia sẻ ngay sau đây sẽ là một cẩm nang cực kỳ hữu ích đối với những ai đang cần và đang quan tâm đến vấn đề này.
Công thức tính chu vi hình tứ giác chính là một trong những kiến thức toán học mà các bạn học sinh rất cần phải nắm vững. Trong bài viết dưới đây chúng tôi sẽ giúp cho tất cả các bạn tổng hợp kiến thức về chủ đề hay là định nghĩa tứ giác và tất cả các kiến thức liên quan, nào hãy cùng tìm hiểu nhé !.
Định nghĩa hình tứ giác
Hình tứ giác chính là một đa giác có 4 cạnh và 4 đỉnh. Tứ giác có thể là một tứ giác đơn (không có cặp cạnh đối nào cắt nhau), hoặc là tứ giác kép (có hai cặp cạnh đối cắt nhau). Tứ giác đơn còn có thể lồi hay lõm.
Tuy nhiên, dù là loại tứ giác nào thì tổng 4 góc của 1 hình tứ giác vẫn sẽ bằng 360 độ. Đây chính là đặc điểm đặc trưng để nhận biết của một hình thuộc hình tứ giác.
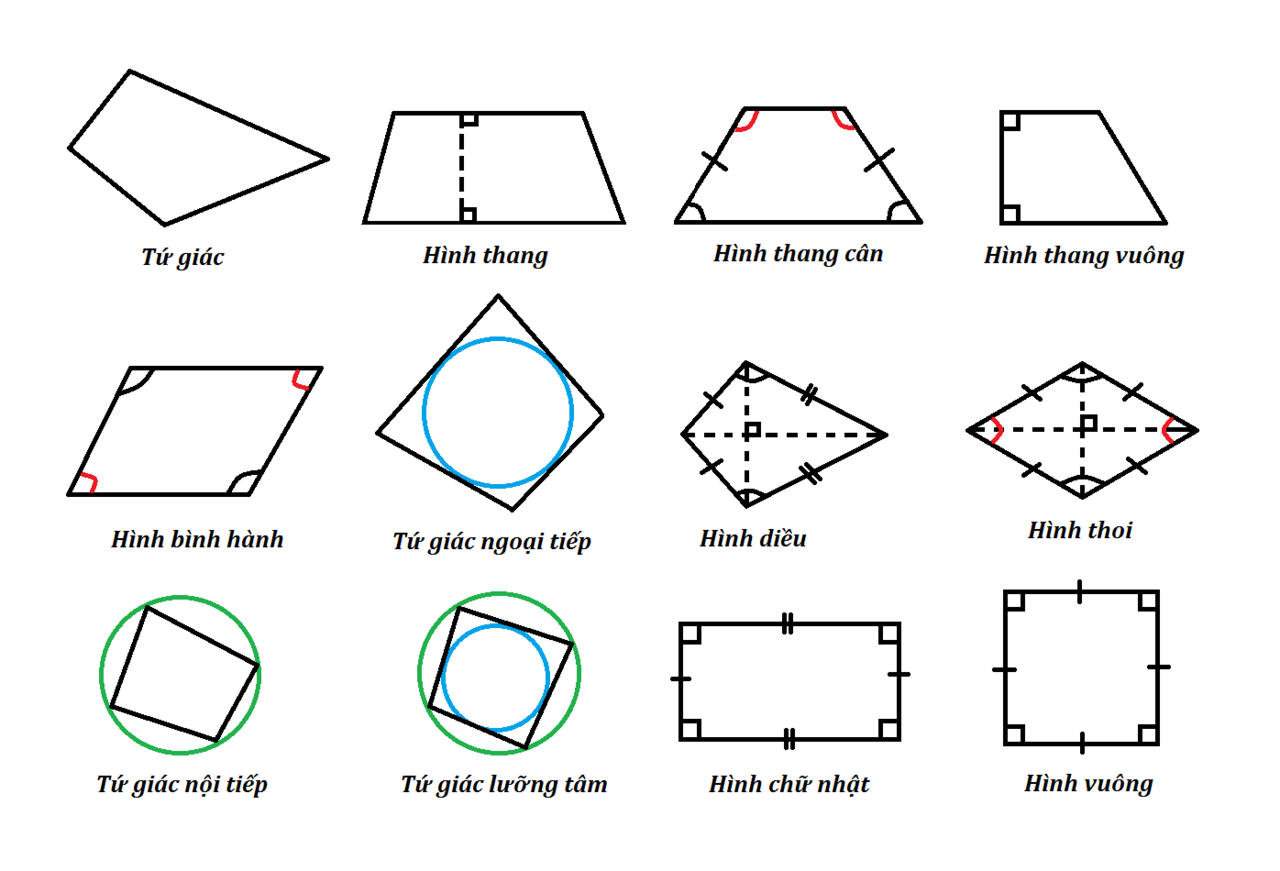
Tứ giác lồi là gì?
Tứ giác lồi chính là tứ giác mà trong tất cả các góc trong nó đều nhỏ hơn tổng 180° và cả hai đường chéo đều được nằm bên trong tứ giác. Hay nói dễ hiểu hơn thì chính là tứ giác lồi là tứ giác luôn nằm gọn trong một nửa mặt phẳng và có chứa bất kỳ cạnh nào.
Tứ giác lõm là gì?
Định nghĩa tứ giác lõm là gì? Tứ giác lõm chính là tứ giác chứa một góc trong có một số đo lớn hơn 180° và một trong hai đường chéo nằm phía bên ngoài tứ giác.
Tứ giác không đều là gì?
Chính là tứ giác mà chính nó không có bất kỳ cặp cạnh nào song song với nhau. Tứ giác thường không đều thường được dùng để đại diện cho tất cả các tứ giác lồi nói chung (không phải là một tứ giác đặc biệt).

Công thức tính chu vi hình tứ giác
Theo định nghĩa này chúng ta đều sẽ có công thức tính chu vi hình tứ giác có rất nhiều loại tứ giác khác nhau như là là tứ giác lồi và tứ giác lõm, tứ giác không đều, tứ giác đều,….
Tứ giác lồi gồm các hình như: hình vuông, hình thang, hình bình hành, hình chữ nhật, hình thoi, tứ giác bất kỳ …. Cách tính diện tích tứ giác cụ thể cho tất cả các trường hợp như sau:
P = a + b + c + d (đvt)
Trong đó: a, b, c, d lần lượt chính là độ dài các cạnh của tứ giác, P chính là chu vi
Ví dụ: Cho tứ giác BDCE có tất cả các cạnh là BD = 2, DC = 3, CE = 4, EB = 5. Yêu cầu tính chu vi hình tứ giác BDCE, đơn vị đo cm.
Giải:
Áp dụng chu vi hình tứ giác, ta có:
P = 2 + 3 + 4 + 5 = 14 (cm)
Tuy nhiên đối với mỗi một hình cũng sẽ có cách tính chu vi riêng.
Hình chữ nhật chính là tứ giác có 4 góc vuông, hai cạnh đối nhau sẽ bằng nhau, cạnh ngắn gọi là chiều rộng, 2 cạnh còn lại được gọi là chiều dài.
Công thức tính của chu vi hình chữ nhật như sau:
C = (a + b) x 2 (đvt)
Trong đó: a là chiều dài, b chính là chiều rộng, C chính là chu vi.
Ví dụ: Cho một hình chữ nhật ABCD có một chiều dài cạnh AB = 6cm và chiều dài cạnh BD = 2 cm. Yêu cầu: hãy tính chu vi của hình chữ nhật ABCD?
Giải:
Ta có AB = a = 6 cm và chiều dài BD = b = 2cm.
Áp dụng công thức tính chu vi hình chữ nhật, ta có như sau:
C = (a + b) x 2 = (6 + 2) x 2= 16 (cm)
Hình vuông chính là tứ giác có tất cả 4 cạnh bằng nhau, 2 cạnh đối song song và bằng nhau, các đường chéo bằng nhau và được vuông góc tại trung điểm.
Công thức tính chu vi của hình vuông như sau
P = a + a + a + a = 4 x a (đvt)
Trong đó: a chính là độ dài các cạnh của hình vuông, P chính là chu vi
Ví dụ: Cho hình vuông ABCD có độ dài cạnh AB = 8 cm. Yêu cầu hãy tính chu vi hình vuông ABCD?
Giải:
Ta có: AB = BC = CD = DA = 8
Áp dụng công thức tính chu vi hình vuông, ta có được như sau:
P = 4 x 8 = 36 (cm)
Hình thang chính là tứ giác có ít nhất 2 cạnh đối nhau song song
Công thức tính chu vi hình thang được tính như sau:
P = a + b + c + d (đvt)
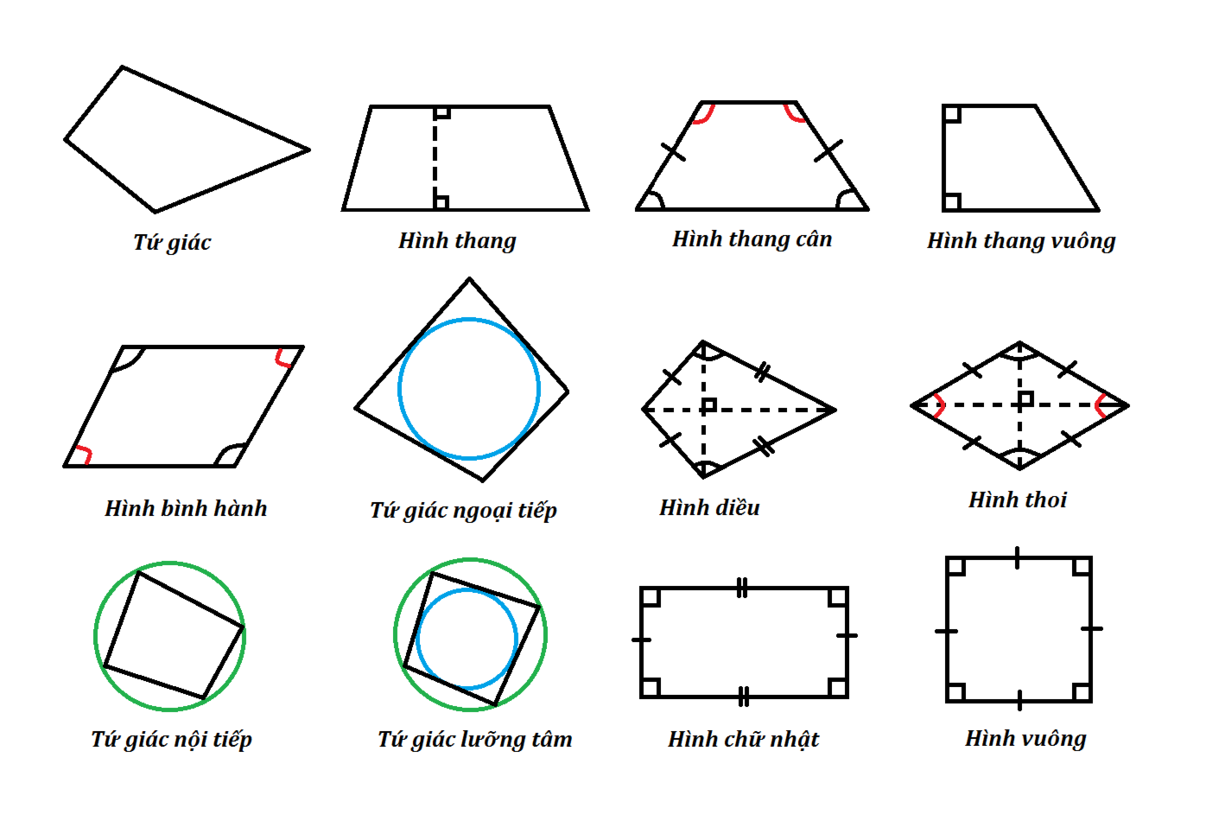
Như vậy trên đây đã chia sẻ đến tất cả bạn công thức tính chu vi hình tứ giác. Tùy vào bài toán và hình tứ giác cụ thể, các bạn hãy lựa chọn cho mình riêng một công thức tính phù hợp nhất. Để hiểu nhiều và nhớ lâu dạng toán này, các ba mẹ cần cho bé rèn luyện thêm nhiều các dạng bài tập thường xuyên.
Hy vọng rằng bài viết sẽ cung cấp được nhiều những kiến thức bổ ích về hình tứ giác giúp các ba mẹ, thầy cô có thể dạy cho các bé! Chúc các bé học tốt chăm ngoan. Cảm ơn tất cả các bạn đã cùng theo dõi bài viết này nhé. Hãy cùng theo dõi để có thể cập nhật thêm cho mình thật nhiều những kiến thức bổ ích khác nhau nhé.









